A 95 Confidence Interval Defines Which of the Following Concepts

Here we will try to cover both the definition as well as what the definition actually implies. Confidence level 1 a.

Confidence Intervals In Statistics Simple Tutorial

Consider for example that for a 95 interval z196 whereas for a 90 interval z1645 So for this factor we have a bit of a tradeoff.

. A 95 confidence interval CI of the mean is a range with an upper and lower number calculated from a sample. They are most often constructed using confidence levels of 95 or 99. However it would be inappropriate to state the following.

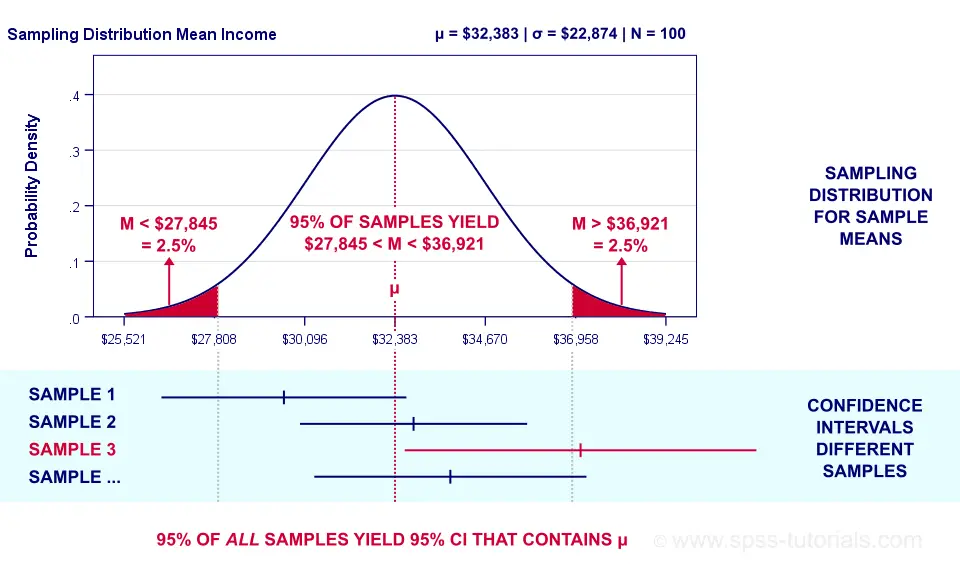
It seems that through various related questions here there is consensus that the 95 part of what we call a 95 confidence interval refers to the fact that if we were to exactly replicate our sampling and CI-computation procedures many times 95 of thusly computed CIs would contain the population mean. For example one may wish to define the limits within which 95 of measurements would be expected to lie with a 95 confidence of being correct. We are 95 confident that the interval between X lower bound and Y upper bound contains the true value of the population parameter.

Variables used to select k. It is tempting to say that if we observe that the two numbers X 196 σ n 1 are for example 5 and 9 then. We are 95 confident that the interval from 0036 to 0064 actually does contain the true value This means that if we were to select many different samples of size 1000 and construct a 95 CI from each sample 95 of the resulting intervals.

Lecture 9 SBCM Joint Program RiyadhSBCM Joint Program Riyadh Example. A confidence interval is a range of values that describes the uncertainty surrounding an estimate. Expected to lie with a given level of confidence.

For example the 90 confidence interval for the number of people of all ages in poverty in the United States in 1995 based on the March 1996 Current Population Survey is 35534124 to 37315094. However we cannot know whether the interval estimate we calculated is. Thus the formula to find CI is.

Where is the sample mean s is the sample standard deviation N is the sample size α is the desired significance level and t1-α2 N-1 is. Because the true population mean is unknown this range describes possible values that the mean could be. You can consider the figure below which indicates a 95 confidence interval.

You can think about the 95 confidence interval for a sample mean as the set of null hypotheses in the class associated with your model which cannot be rejected p005 and are therefore in a probabilistic sense compatible with your data. A Construct a 95 confidence interval for the the mean annual gas consumption for houses with standard insulation. The parameter q is also called the confidence level.

For example a 95 confidence interval means that in the long run 95 of confidence intervals constructed in this manner will contain the true parameter. Your desired confidence level is usually one minus the alpha a value you used in your statistical test. DANGER Pr 5 μ 9 095.

The concept of a 95 Confidence Interval 95 CI is one that is somewhat elusive. Parameter 1001 𝛼 of the time. The commonly used confidence level is 95 confidence level.

It is estimated from the original sample and usually defined as 95 confidence but it may differ. Confidence limits are defined as. We want a high confidence level but not so high as to produce such a wide interval as to be useless.

However other confidence levels are also used such as 90 and 99 confidence levels. If multiple samples were drawn from the same population and a 95 CI calculated for. To find that you set a 95 confidence level and find that the 95 confidence interval is 168182.

The confidence interval is based on the mean and standard deviation. Put the two numbers in and use a comma then a space between the two numbers. Different types of CrIs 95 could be constructed eg equal-tail intervals where 25 probability of the location of the true effect is below the lower interval limit and 25 is above the upper limit.

P hat ME for 95 CI If p hat 038 and ME for 95 CI 0096 what is CI. Keep the numbers in 3 decimal places. To say that there is 95 confidence is shorthand for 95 of all possible samples of a given size from this population will result in an interval that captures the unknown.

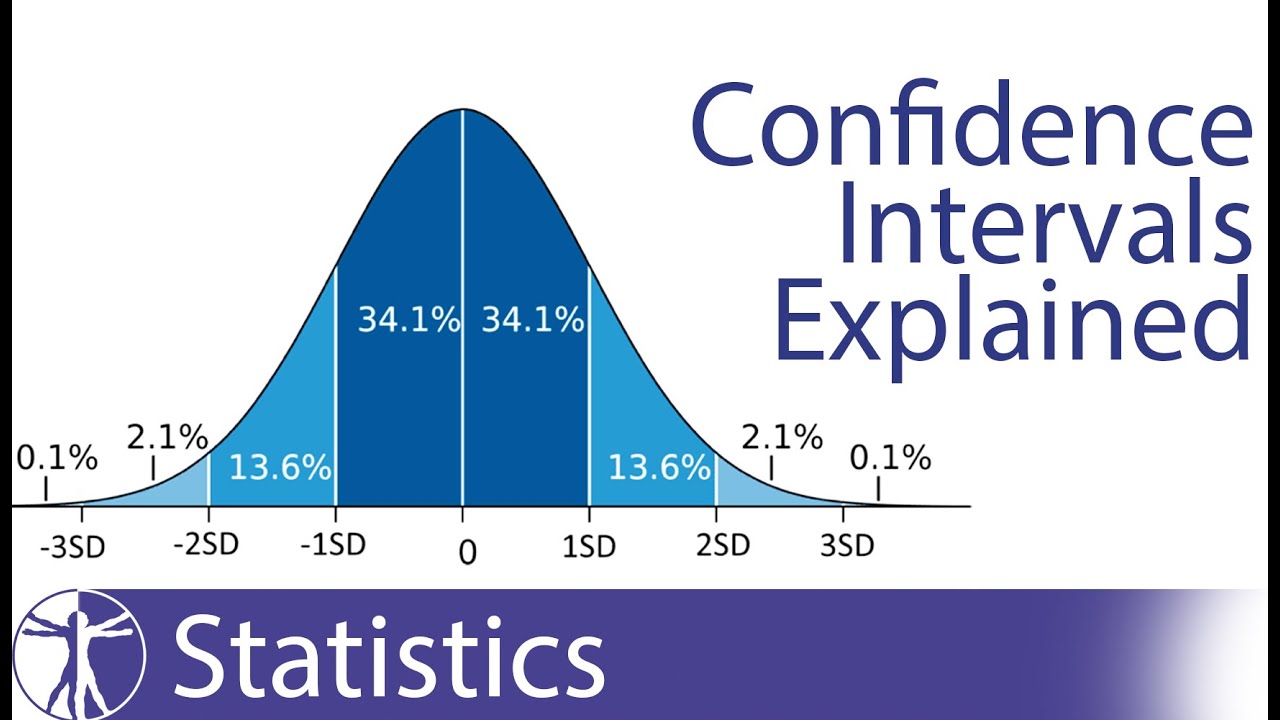
1 X 196 σ n 1. Is a 95 confidence interval for μ. A 95 confidence level means that 95 of the intervals would include the population parameter.

This means that a q-percent confidence interval has a probability of q100 of containing the population parameter. It is the range in which the values likely to exist in the population. X Zα2 σ n Where.

005 0036 0064 Correct. Some R output that may help. The interval whose endpoints are.

Confidence intervals are often used in conjunction with point estimates to highlight the. Confidence intervals measure the degree of uncertainty or certainty in a sampling method. To construct a 95 Confidence Interval we use the following formula.

There is a 95 probability that the interval between X lower bound and Y upper bound contains the true value of the population parameter. Mostly the confidence level is selected before examining the data. The confidence interval CI is a range of values around the mean that estimate the value in which an unknown parameter lies.

We indicate a confidence interval by its endpoints. The interval is symmetrical and is computed using the expression. Or the highest posterior density interval HPD it may not have equal tails but it is the shortest interval encompassing 95 of the probability and any point contained within the interval.

P1 qt p1 8 1 -2896 -2306 -1860 -1397 1397 186O 2306 2896 qt p1 9 1 -2821 -2262 -1833 -1383 1383 1833 2262 2821. The statement above is the. Explore the definition of a CI how to calculate a CI using the mean.

For example lets suppose you were surveying an average height of men in a particular city. A 95 confidence interval CI of the mean is a range with an upper. Thus a 95 confidence interval for the mean μ is a random interval that contains μ with probability 095.

This is primarily due to the fact that many students of statistics are simply required to memorize its definition without fully understanding its implications. Thats why 95 is the most common confidence level used. X ks where k depends on three things.

What if were able to use a normal model. For example if you construct a confidence interval with a 95 confidence level you are confident that 95 out of 100 times the estimate will fall between the upper and lower values specified by the confidence interval. But suppose we take a.

That is for a 95 confidence interval if many samples are collected and the confidence interval computed in the long run about 95 of these intervals would contain the true mean.

Understanding Confidence Intervals Easy Examples Formulas

Confidence Intervals Explained Calculation Interpretation Youtube

What Are Confidence Intervals Simply Psychology

Share this post